Análisis de datos PCR/qPCR
- Análisis cualitativo de la PCR/qPCR
- Análisis de datos de la qPCR
- Obtención de valores Cq precisos
- Configuración del umbral
- Estrategias de cuantificación de qPCR
- Cuantificación de curvas estándar
- Cuantificación relativa/comparativa
- Normalización
- Selección del gen de referencia
- Análisis de la estabilidad del gen de referencia
- Métodos de normalización alternativos
- Análisis estadístico y visualización de datos
- Técnicas de visualización para el análisis univariante
- pruebas estadísticas
- Conglomeración jerárquica
- Análisis de componentes principales
PCR/qPCR Análisis Cualitativo de Datos
Una vez finalizada una PCR tradicional, los datos se analizan mediante resolución a través de un gel de agarosa o, más recientemente, a través de un sistema de electroforesis capilar. Para algunas aplicaciones, se ejecutará una qPCR con los datos de punto final utilizados para el análisis, como para el genotipado SNP. En cada caso, los datos de punto final proporcionan un análisis cualitativo después de que la PCR haya alcanzado la fase de meseta. En algunos casos, puede ser posible analizar los datos de punto final para realizar un análisis semicuantitativo del rendimiento de la PCR, pero las mediciones cuantitativas se realizan más a menudo utilizando la qPCR y el análisis de los valores del ciclo de cuantificación (Cq)1 valores.
Análisis de datos de qPCR
A lo largo de esta guía se han destacado los factores que contribuyen a las variaciones en la medición de ácido nucleico mediante PCR o qPCR. Cada uno de estos factores debe optimizarse para dar como resultado un ensayo que proporcione el valor más cercano posible a la cantidad real de gen (diana) en la reacción. El resultado de estos procesos es la generación de un conjunto de valores de Cq para cada diana en cada muestra. En este capítulo se presenta el proceso de obtención y análisis de esos valores de Cq para proporcionar datos fiables que representen la historia biológica.
Derivación de valores precisos de Cq
Corrección de la línea de base
Se determina un valor Cq para cada objetivo en cada muestra. Diferentes paquetes de análisis que están asociados con diferentes instrumentos, tienen enfoques alternativos para determinar el Cq (y también utilizan nombres alternativos, por ejemplo, Ct, Cp, take off point). Está fuera del alcance de esta guía profundizar en los detalles de todos estos algoritmos. Sin embargo, las mediciones de qPCR basadas en curvas de amplificación son sensibles a la fluorescencia de fondo. La fluorescencia de fondo puede deberse a una serie de factores, entre los que se incluyen la elección del material plástico, la fluorescencia restante de la sonda que no se apaga, la luz que se filtra en el pocillo de la muestra y las diferencias en la detección óptica de un pocillo determinado de la placa de microtitulación. En ensayos bien diseñados, el fondo es bajo en comparación con la señal amplificada. Sin embargo, la variación de la señal de fondo puede dificultar la comparación cuantitativa de diferentes muestras. Por lo tanto, es importante corregir las variaciones de fluorescencia de fondo que causan diferencias en la línea base (Figura 10.1).
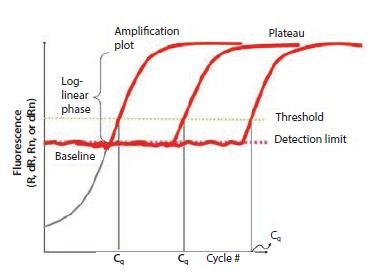
Figura 10.1Los componentes de los gráficos de amplificación. Este gráfico muestra el aumento de la fluorescencia con el número de ciclos para diferentes muestras. El umbral se fija por encima del límite de detección, pero muy por debajo de la fase de meseta durante la cual la tasa de amplificación se ralentiza.
Un enfoque común es utilizar la intensidad de fluorescencia durante los primeros ciclos, como entre los ciclos 5 a 15, para identificar un componente constante y lineal de la fluorescencia de fondo. Esto se define entonces como el fondo o línea de base para el gráfico de amplificación. Debido a los efectos transitorios, es aconsejable evitar los primeros ciclos (por ejemplo, los ciclos 1 a 5) para la definición de la línea de base, ya que a menudo muestran artefactos de estabilización de la reacción. Cuantos más ciclos se utilicen para la corrección de la línea de base, mayor será la precisión potencial del componente lineal de las variaciones de la línea de base. Muchos paquetes de software de instrumentos permiten el ajuste manual de los ciclos que deben considerarse para la definición de la línea de base. El usuario debe explorar estas funciones y resistirse firmemente a la tentación de aceptar los ajustes predeterminados.
Un ejemplo del efecto del ajuste de la línea de base se muestra en la Figura 10.1. Como puede verse, los valores de Cq y la forma aparente del gráfico de amplificación se ven afectados por el ajuste preciso de la línea de base. En el ejemplo, la línea de base para la curva etiquetada C3 se ha ajustado manualmente de forma incorrecta, de modo que los ciclos de la línea de base calculados a partir de los datos en los ciclos 5 a 31. Esto hace que la curva baje al nivel de línea base cero (Figura 10.2A) con un Cq de 28,80. Para corregir esto, se visualizan los datos brutos, R, y se identifica el último ciclo del fondo lineal (el último ciclo antes de la amplificación). En Figura 10.2B, puede verse que se trata del ciclo 22. La línea de base se establece correctamente en cero entre el ciclo 5 y el ciclo 22 (Figura 10.2C), y el gráfico de amplificación se corrige a continuación (Figura 10.2D). El Cq corregido es 26,12. Por lo tanto, nótese que había una diferencia sustancial entre los valores de Cq con las configuraciones de líneas de base incorrectas y correctas, lo que demuestra que establecer la línea de base correcta es un componente importante del análisis de datos.
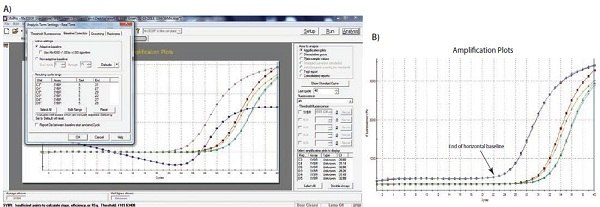
Figura 10.2A-B. A)Ejemplo típico de datos que caen por debajo de la lectura de fluorescencia normalizada a cero cuando el ajuste de la línea de base es incorrecto (gráfico de amplificación azul). B) Datos brutos de los mismos gráficos de amplificación que muestran el límite de la línea de base lineal y que los datos no son erróneos.
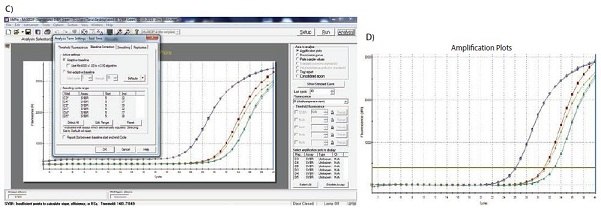
Figura 10.2C-D. C)Los límites del inicio y el final de la línea de base se definen mediante los ajustes adecuados del software. D) La aplicación de la configuración corregida de la línea de base da lugar a datos de buena calidad
Establecimiento del umbral
Aunque algunos investigadores abogan por trazar mapas de amplificación individuales para estimar la eficiencia de amplificación y las cantidades objetivo en muestras medidas2,3,4, el enfoque original y más común para derivar la Cq es utilizar un umbral. Es probable que la amplia adopción de este enfoque se deba a que el método de umbral es un método de cuantificación simple y eficaz.
El principio que subyace al método de umbral es que; para visualizar la señal fluorescente asociada de la amplificación qPCR, la señal debe aumentar de modo que esté por encima del límite de detección del instrumento (y, por lo tanto, de la línea de base; Figura 10.1). El número de ciclos necesarios para que esto ocurra es proporcional al número inicial de copias de la diana en la muestra. Por lo tanto, se requieren más ciclos para que la señal aumente por encima de la línea de base si el número de copias original es bajo y menos ciclos si el número de copias es alto. Dado que la línea de base se fija en el límite de detección del sistema, las mediciones en la línea de base serían muy imprecisas. Por lo tanto, en lugar de medir hasta la intensidad de fluorescencia mínima que el sistema puede detectar, se selecciona una fluorescencia más alta y se introduce un umbral artificial.
La selección de la intensidad umbral requiere el cumplimiento de algunos principios fundamentales. Es importante que el umbral se establezca a una intensidad fija para un objetivo determinado y para todas las muestras que se van a comparar. Si hay demasiadas muestras para que quepan en una sola placa, debe adoptarse un esquema de calibración entre placas, por ejemplo, la inclusión de un control replicado que sirva como control entre placas o una dilución en serie de la curva estándar. En teoría, el umbral puede fijarse en cualquier punto de la fase log-lineal de la curva de amplificación. Sin embargo, en la práctica, la fase logarítmica lineal de la amplificación puede verse alterada por la deriva de la línea de base de fluorescencia de fondo, la fase de meseta o las diferencias en la eficacia del ensayo y, por tanto, el gradiente de la trama de amplificación a ciclos más altos. Se recomienda que el umbral se establezca de la siguiente manera:
- Suficientemente por encima de la línea base de fluorescencia de fondo para tener la seguridad de evitar que la trama de amplificación cruce el umbral prematuramente debido a la fluorescencia de fondo.
- En la fase logarítmica del gráfico de amplificación, donde no se ve afectado por la fase de meseta (esto se aprecia más fácilmente visualizando los gráficos de amplificación en una vista logarítmica, Figura 10.3A).
- En una posición en la que las fases logarítmicas de todos los gráficos de amplificación son paralelas.
El proceso de establecimiento del umbral se demuestra en la Figura 10.3. En la Figura 10.3A, los gráficos de amplificación se visualizan en una escala logarítmica del eje Y, proporcionando así una expansión visual de la fase logarítmica de amplificación y presentando esto como una porción lineal del gráfico de amplificación. El umbral se establece en la intensidad de fluorescencia más alta (referirse al eje Y) que se encuentra dentro de esta fase logarítmica y en la que todos los gráficos de amplificación son paralelos. La escala se devuelve entonces a la vista lineal (Figura 10.3B) mostrando el ajuste más alto que cumple los requisitos de ajuste del umbral. Alternativamente, el umbral puede fijarse en el extremo inferior de esta fase logarítmica (Figuras 10.3C y 10.3D). Siempre que la fase logarítmica de las gráficas de amplificación sean paralelas, el ΔCq entre muestras no se ve afectado por el ajuste del umbral.
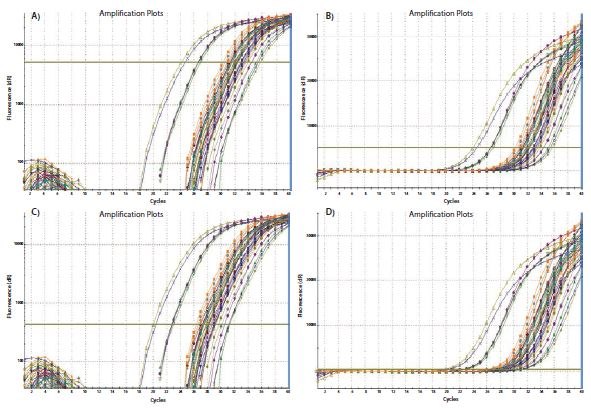
Figura 10.3El ajuste del umbral influye en el Cq absoluto registrado y puede influir en el ΔCq entre muestras. A). Utilizando un gráfico logarítmico frente a lineal de los datos, el umbral se establece en la intensidad de fluorescencia más alta pero donde los gráficos de amplificación muestran fases logarítmicas paralelas. B). El ajuste del umbral se mantiene desde A) y se muestra en el gráfico lineal vs lineal. C). Utilizando un gráfico logarítmico frente a lineal de los datos, el umbral se establece en la intensidad de fluorescencia más baja pero donde los gráficos de amplificación muestran fases logarítmicas paralelas. D). El ajuste del umbral se mantiene a partir de C) y se muestra en el gráfico lineal frente a lineal. En cada caso, los valores ΔCq entre las muestras son los mismos.
El requisito de establecer un umbral en una posición en la que las fases logarítmicas lineales de los gráficos de amplificación sean paralelas se hace más pertinente cuando se incluyen en el análisis datos de ciclos más altos. El procedimiento de ajuste del umbral que se describió para los datos de la Figura 10.3 se repitió en un conjunto de datos de mayor Cq y los resultados se presentan en la Figura 10.4. Los datos resultantes de Cq en Tabla 10.1.1 sirven para ilustrar la variabilidad de los valores de Cq y, lo que es más importante, de ΔCq para tres parcelas de amplificación con tres ajustes de umbral (Figura 10.4). Los valores ΔCq y, por lo tanto, la estimación de la cantidad relativa de diana en cada muestra dependen en gran medida del ajuste del umbral (Figura 10.4) porque las parcelas de amplificación no son paralelas.
Cq valores ΔCq .

Figura 10.4.El análisis que se realizó y demostró en la Figura 10.3 se repitió utilizando un conjunto de datos diferente. En este caso, las gráficas de amplificación no son paralelas debido a una diferencia en la eficiencia de la reacción a Cq alto. Los ajustes más bajos para A) y B) dan como resultado valores de ΔCq diferentes que los ajustes más altos para C) y D) (resumidos en la Tabla 10.1).
Estrategias de cuantificación de qPCR
Para una cuantificación fiable es imprescindible establecer con precisión la línea base y el umbral. Tras ajustar cada uno de ellos, se genera un valor Cq que se utiliza como base para la cuantificación. La cantidad de diana en una muestra dada se determina entonces utilizando una curva estándar o una cuantificación relativa/comparativa.
Cuantificación por curva estándar
Como su nombre indica, la cuantificación por curva estándar requiere el uso de una curva estándar para determinar las cantidades de dianas en las muestras de ensayo. Todas las cantidades determinadas para las muestras son, por lo tanto, relativas a la cantidad asignada a la curva estándar. Para ello, es necesario ejecutar estándares externos adicionales junto con cada conjunto de reacciones de muestras. La elección del material para la curva estándar es importante para eliminar posibles diferencias en la cuantificación debidas a diferencias entre las eficiencias de ensayo en las muestras y en los estándares. Los sitios de unión del cebador de los estándares externos deben ser los mismos que los de la diana, contener secuencias iguales a las de la diana, tener una complejidad similar y manipularse de la forma más parecida posible. Por lo tanto, cuando se mide la concentración de una diana en el ADNc, es preferible medir el mismo ADNc en una dilución en serie de una muestra de control. Sin embargo, en algunos estudios hay razones prácticas que lo impiden, por lo que es importante reproducir las condiciones de la muestra de la forma más parecida posible, por ejemplo, añadiendo ADNg de una especie no relacionada con la especie de ensayo, a un estándar de oligonucleótidos artificial o a un plásmido linealizado que lleve la secuencia estándar. Una vez identificado un constructo o amplicón adecuado, se genera una curva estándar de diluciones seriadas. La Cq de la diana se determina para cada uno de los estándares y se representa gráficamente frente a la concentración o el factor de concentración/dilución relativo en una escala logarítmica. El resultado es una curva estándar que se utiliza para determinar las concentraciones de las muestras de ensayo por comparación de los valores Cq derivados de la amplificación de las muestras desconocidas. Cuando se utiliza una curva estándar para la cuantificación, el ajuste del umbral debe mantenerse constante para la determinación de Cq para el estándar y para las muestras en la misma placa. El umbral puede diferir entre placas.
Cuantificación relativa/comparativa
La cuantificación relativa o comparativa utiliza la diferencia en Cq como determinante de las diferencias en la concentración de la secuencia diana en diferentes muestras. En lugar de medir cantidades de diana por muestra como con el método de la curva estándar, esto conduce a conjuntos de datos que muestran cambios de pliegues entre muestras.
En la forma original de este enfoque5, se suponía que la eficacia de todos los ensayos era del 100 %, lo que llevaba a suponer que un Cq diferencia de 1 (ΔCq = 1) era el resultado de una diferencia de 2 veces en la diana. Para determinar un cambio de pliegue en la diana o en el gen de interés (GOI), los datos también deben referenciarse a un control de carga (gen de referencia, ref; véase a continuación una discusión relativa a la normalización de los datos).
Control de carga.
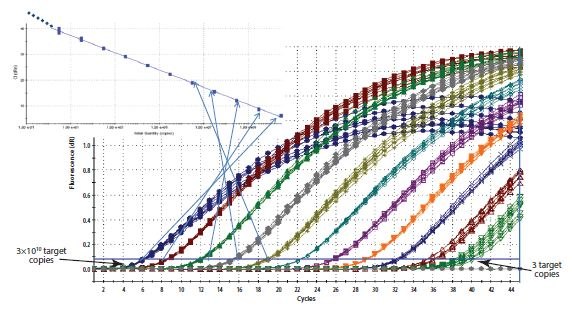
Figura 10.5.Construcción de una curva estándar. El Cq registrado para cada muestra de una serie de diluciones se traza en una escala logarítmica lineal frente a la concentración relativa.
En la ecuación 1, la relación de la GOI, después de la corrección al gen de referencia, en 2 muestras (A con respecto a B) se mide como: 2 (suponiendo un 100% de reacciones eficientes) elevado a la potencia de las diferencias en los valores de Cq para el GOI dividido por 2 elevado a la potencia de las diferencias en los valores de Cq para el gen de referencia

Ecuación 1.Modelo de cuantificación relativa original (Livak).
Sin embargo, como se ilustra en Optimización y validación de ensayos, las eficiencias de las reacciones varían considerablemente y esto puede tener un gran impacto en los datos. Por lo tanto, se abordaron los supuestos de la Ecuación 1 (Ecuación 2)6, de modo que las diferencias en las eficiencias de reacción pudieran incorporarse a los análisis. En este caso, el factor de amplificación 2 se sustituye por la eficiencia real de la PCR (determinada mediante un análisis de la curva estándar; véase Optimización y validación de ensayos).

Ecuación 2.Modelo de cuantificación relativa adaptado a la eficacia (Pfaffl)
Como ejemplo del uso del modelo de cuantificación relativa adaptado a la eficiencia (Ecuación 2), se presenta un conjunto de valores de Cq en la Tabla 10.2. La eficacia para el GOI es de 1,8 y para el gen de referencia de 1,94.
La eficacia para el GOI es de 1,8 y para el gen de referencia de 1,94.
Este es un ejemplo muy simple de un estudio con el requisito de medir la diferencia de pliegues entre un gen en dos muestras y después de la normalización a un único gen de referencia. La relación muestra el cambio de pliegue del GOI en la muestra 2 en relación con la muestra 1, después de la corrección al gen de referencia único. Sin embargo, se ha hecho evidente que la selección de un único gen de referencia adecuado es a menudo imposible y, por lo tanto, se han sugerido enfoques más sofisticados para la normalización.
Normalización
El principal objetivo de la mayoría de los experimentos basados en PCR es responder a la pregunta básica de si la diana está presente en la muestra (desconocida, UNK). En el nivel más simple, esto se responde corriendo un gel y examinando los fragmentos para detectar la presencia o ausencia de la GOI deseada. Cuando el fragmento está presente, la confirmación del tamaño del fragmento garantiza un resultado positivo. Sin embargo, cuando está ausente, existe la posibilidad de un resultado falso negativo. Por lo tanto, es fundamental repetir el ensayo de prueba y también realizar al menos una PCR adicional que sirva como control de carga y PCR positiva. El ensayo de control de inhibición universal, SPUD (véase Purificación de muestras y evaluación de la calidad), puede utilizarse para respaldar la confianza en un resultado negativo. Un enfoque alternativo consiste en realizar un ensayo específico para un gen o genes de referencia. Tradicionalmente, los ensayos de PCR que detectan los genes de referencia, GAPDH, ARN ribosómico 18S o β actina se realizaban junto con los de la GOI y los fragmentos resultantes se visualizaban en un gel. La GAPDH, el ARN ribosómico 18S y la β actina se expresan de forma constitutiva, por lo que se utilizaron como controles de carga en los análisis semicuantitativos. Sin embargo, pronto se hizo evidente que estos genes no se expresan de forma ubicua en la misma concentración en todas las células, independientemente del diseño experimental. Por lo tanto, surgió la necesidad de una referencia estable cuando el objetivo era medir concentraciones relativas de ácidos nucleicos, normalmente ADNc pero también ADNg cuando, por ejemplo, se examinaba la variación del número de copias de un gen.
La normalización es el proceso de corrección de las mediciones técnicas a una referencia estable para examinar la verdadera variación biológica. Existen muchos métodos para normalizar las diferencias técnicas, lo que significa que debe seleccionarse y validarse el enfoque adecuado para el experimento específico7. Es fundamental reconocer que la adopción de técnicas de normalización inadecuadas puede ser más perjudicial para el proceso analítico global que no normalizar en absoluto8.
El efecto de la calidad de la muestra en la normalización del ensayo
El efecto de la integridad y pureza de la muestra en las mediciones de la cantidad diana mediante qPCR y RT-qPCR se debatió ampliamente (Purificación y evaluación de la calidad de las muestras, Control de calidad de las muestras y Transcripción inversa, Transcripción inversa). Se demostró que los inhibidores en la muestra y la degradación del ARN tienen un efecto diferencial en la medición de una diana determinada9. Los inhibidores afectan a la medición de cualquier diana, pero en distinto grado, dependiendo del diseño del ensayo. La degradación del ARN total afecta a la medición de ARNm y miARN10, y también depende en gran medida del diseño experimental general. Por lo tanto, es fundamental tener en cuenta el efecto de la concentración de molde en la reacción de RT y el efecto de la calidad de la muestra en los datos después de la normalización. La normalización no contrarrestará el efecto de ensayos o muestras de baja calidad (véase Optimización y validación de ensayos).
Enfoques de normalización
En principio, los métodos de normalización contrarrestan la variabilidad que puede introducirse durante el proceso de múltiples pasos que se requiere para realizar un análisis de qPCR (Figura 10.6). Sin embargo, la aplicación de la normalización en cualquier etapa del proceso puede no controlar el error técnico y/o el sesgo que se introdujo, o se introducirá, en una etapa anterior o posterior, respectivamente. Los métodos de normalización no se excluyen mutuamente, por lo que se recomienda adoptar una combinación de controles11.
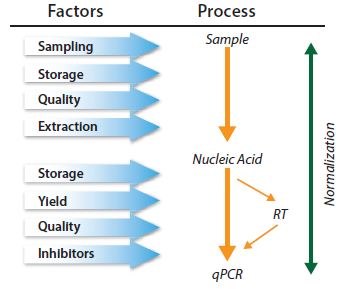
Figura 10.6.La qPCR es un proceso de varios pasos y cada uno de ellos debe controlarse. La normalización debe considerarse dentro de una serie de controles.
El objetivo de la normalización es proporcionar un punto de referencia estable al que se puedan referir las mediciones; por lo tanto, la elección del factor de normalización debe ser una medición que sea estable a lo largo del experimento. Puede tratarse de gen(es) de referencia estable(s), o de una de las alternativas, como el número de células, la masa tisular, la concentración de ARN/ADN, un pico externo12, o una medida representativa de los genes expresados globalmente.
Selección de genes de referencia
Los genes de referencia son objetivos cuya cantidad no cambia como resultado del experimento. Cuando se cuantifica la variación del número de copias de ADN en la que el número de copias de la secuencia de interés puede cambiar, la medición se normaliza simplemente dirigiéndose a una región genómica alternativa que se sabe que no cambia. Un ejemplo de cómo se puede aplicar esto es cuando se mide la amplificación genómica del Receptor 2 del Factor de Crecimiento Epidérmico Humano (HER-2). La inestabilidad genómica del HER-2 es un indicador pronóstico en el cáncer de mama y la medición precisa del estado de amplificación del HER-2 es importante para el tratamiento de las pacientes. El estado de HER-2 puede medirse mediante qPCR comparando las copias de HER-2 con otra diana genómica que actúa como control.
Cuando se mide la expresión génica, los genes de referencia son dianas con concentraciones de ARNm que no cambian como resultado del experimento. Un ejemplo de estudio sería aquel en el que se está midiendo el efecto sobre la expresión del gen X tras la adición de un compuesto mitogénico a una monocapa celular. Se necesita un punto de referencia para medir el cambio en el gen X. Por lo tanto, también se mide otro gen (o genes) que se sabe que no se ven afectados por el mitógeno en cuestión. Esto proporciona al investigador el reto inmediato de encontrar una diana de ARNm que no se vea afectada por el procedimiento experimental, antes de poder estudiar el GOI. Este proceso de validación de genes de referencia es fundamental para una medición precisa de la GOI. El enfoque más utilizado para la normalización es ignorar este proceso y normalizar los datos de expresión génica a un único gen de referencia no validado. Esta práctica no se recomienda y se opone directamente a las directrices del MIQE1. La cuantificación de ARNm por RT-qPCR se ha visto rutinariamente comprometida por la elección incorrecta de genes de referencia. No es aceptable seguir las prácticas relativamente comunes de utilizar un gen de referencia porque los cebadores ya están en el congelador, se utilizó históricamente en Northern blots, lo utiliza un colega, o se utiliza en otro laboratorio para un experimento diferente. Los genes de referencia deben validarse en escenarios experimentales específicos para tener la seguridad de que el gen de referencia en cuestión no se ve afectado por el experimento. Si no se lleva a cabo esta validación y el gen de referencia se ve afectado por el experimento, los resultados podrían ser incorrectos y es probable que las interpretaciones posteriores den lugar a datos sin sentido8.
Existen diversas publicaciones científicas que describen diferentes métodos de normalización7-14 así como una plétora de publicaciones que describen los protocolos necesarios para identificar los genes normalizadores más apropiados para un escenario experimental determinado. Mientras que en el pasado, una cuestión clave era si seleccionar genes de referencia únicos o múltiples, los menores costes de funcionamiento implican que las mejores prácticas actuales se han desplazado hacia la medición de genes de referencia múltiples.
La selección de genes de referencia estables requiere que el analista evalúe la estabilidad de la qPCR para un número (normalmente de 10 a 20 genes) de dianas de ARNm candidatas7 en un subconjunto de muestras que representen los ARNm de prueba y de control. Encontrará un protocolo completo en Apéndice A, Protocolos, de esta guía y puede utilizarse en combinación con diferentes métodos analíticos mediante programas como REST15, GeNorm14, Bestkeeper16 o NormFinder17. Este procedimiento se describe con más detalle en la siguiente sección, Análisis de la estabilidad del gen de referencia.
Análisis de la estabilidad del gen de referencia
El gen de referencia es literalmente el punto de pivote de los ensayos de cuantificación relativa por qPCR. Por lo tanto, es fundamental para la fiabilidad de todo el ensayo que el gen de referencia sea estable. Si la expresión del gen de referencia varía entre las muestras, la variación se transferirá directamente a los resultados de cuantificación y la variabilidad añadida puede oscurecer el efecto biológico observable deseado o, peor aún, puede crear una apariencia totalmente artificial de un efecto biológico, que no esté relacionado con el gen de interés real. Por estas razones, se recomienda encarecidamente que se sigan varias medidas de seguridad para que la variabilidad del gen de referencia sea insignificante y para que las medidas de los efectos biológicos sean lo más significativas posible.
Discutiblemente, la medida de seguridad más importante es utilizar no sólo uno, sino dos o más genes de referencia. La expresión de varios genes de referencia puede promediarse para reducir la variabilidad técnica debida a la normalización. Esto puede ser útil para mejorar la significación en mediciones de pequeños efectos biológicos. Sin embargo, lo que es más importante, dos o más genes de referencia proporcionan controles mutuos para mantener la estabilidad y el control de sucesos inesperados que puedan influir en los niveles de expresión de uno de los genes de referencia. Con un único gen de referencia, existe el riesgo de que las influencias inesperadas de la expresión génica no se detecten en el ensayo.
Otra medida de seguridad es utilizar más de un método para identificar genes de referencia estables. El siguiente es un ejemplo para ilustrar varios aspectos de la normalización de genes de referencia, incluida una posible ventaja de utilizar tanto los métodos geNorm como NormFinder en el mismo conjunto de datos.
Tabla 10.3 contiene una lista de genes de referencia candidatos que se evaluaron durante un taller que realizamos previamente con el EMBL. Se recogieron muestras de un cultivo de células humanas en dos grupos de tratamiento diferentes. Este conjunto de datos se utilizará para demostrar aspectos de la validación de genes de referencia.
Tanto el algoritmo NormFinder como el geNorm se han desarrollado con la suposición de que la prueba de una multitud de candidatos a genes de referencia puede utilizarse para clasificar la estabilidad de los candidatos a genes de referencia individuales. Este supuesto puede ser cierto si, por ejemplo, todos los genes de referencia candidatos varían estocásticamente en torno a niveles de expresión estables. Sin embargo, esto puede no ser necesariamente cierto en la realidad. Por lo tanto, para evitar resultados engañosos, es prudente evitar los genes de referencia candidatos regulados y, en particular, corregulados.
Evitar los genes de referencia candidatos regulados y, en particular, corregulados.
La lista de genes de referencia candidatos mostrada en Tabla 10.3 fue elegida específicamente para seleccionar genes que pertenecen a diferentes clases funcionales, reduciendo la posibilidad de que los genes puedan estar co-regulados. Una excepción notable es GAPDH, que está presente aquí en dos versiones. Aunque esto no afecta a este análisis, la mejor práctica es evitar múltiples entradas de genes que puedan ser sospechosos de estar co-regulados.
El primer algoritmo que se demostrará es geNorm. Este algoritmo proporciona una evaluación de la estabilidad de los genes mediante el cálculo de una medida de estabilidad de genes denominada valor M, que se basa en comparaciones por pares entre el candidato a gen de referencia analizado y todos los demás candidatos a gen de referencia del conjunto de datos. Se realiza de forma iterativa, lo que significa que en este ejemplo, el procedimiento se realiza primero en los 15 candidatos a genes de referencia, se elimina el menos estable, se repite el proceso en los 14 restantes, se elimina el segundo candidato menos estable, y así sucesivamente hasta que queden dos genes de referencia.
Puede haber ocasiones en las que la identificación del gen de referencia más estable puede ser particularmente desafiante. Un caso puede ser cuando todos los candidatos a gen de referencia tienen un rendimiento bajo. Otro caso puede ser si todos los genes de referencia candidatos tienen un buen rendimiento. Para distinguir entre estos dos casos, una pauta útil es que los genes de referencia con un valor M inferior a 0,5 pueden considerarse expresados de forma estable.
El segundo algoritmo que se demostrará es NormFinder, que es un paquete de análisis de genes de referencia disponible gratuitamente (Apéndice B, Recursos adicionales). El algoritmo subyacente adopta un enfoque similar al ANOVA para la evaluación de la estabilidad del gen de referencia, en el sentido de que se analizan las variaciones de la totalidad y de los subgrupos. Una ventaja de esto es que las medidas obtenidas están directamente relacionadas con los niveles de expresión génica. Por lo tanto, una desviación estándar de 0,20 en Cq unidades representa aproximadamente un 15% de variación en los niveles de expresión del número de copias del candidato a gen de referencia en particular.
Para mayor comodidad, en esta demostración, se accede a ambos paquetes de análisis utilizando el software de análisis de datos GenEx (MultiD), pero también están disponibles como paquetes independientes (Apéndice B, Recursos adicionales).
Los diagramas de barras mostrados en la Figura 10.7 ilustran los genes de referencia clasificados según sus respectivas medidas de estabilidad utilizando ambos algoritmos. Además, un gráfico que muestra la desviación estándar acumulada de NormFinder indica que una combinación de hasta los tres mejores genes de referencia puede producir mejoras en la estabilidad.
La desviación estándar acumulada de NormFinder indica que una combinación de hasta los tres mejores genes de referencia puede producir mejoras en la estabilidad.

Figura 10.7.Diagramas de barras que muestran las medidas de estabilidad: Valores M para geNorm y desviaciones estándar para NormFinder. Además, un gráfico que muestra la desviación estándar acumulada de NormFinder indica que una combinación de hasta los tres mejores genes de referencia puede producir mejoras en la estabilidad. El conjunto de datos se generó a partir de ensayos diseñados para los genes de referencia candidatos mostrados en la Tabla 10.3 y medidos en un cultivo de células humanas en dos grupos de tratamiento diferentes. Obsérvese que, en este caso, los algoritmos de estabilidad del gen de referencia geNorm y NormFinder no se ponen de acuerdo sobre los mejores genes de referencia.
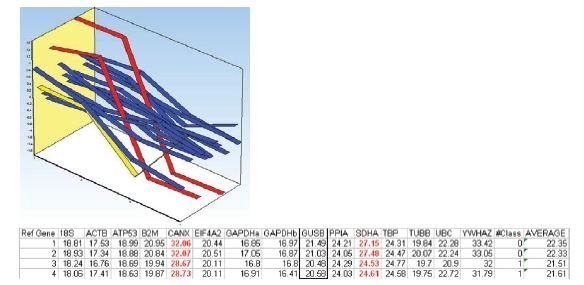
Figura 10.8.Perfil de expresión centrado medio de los genes candidatos de referencia de las dos muestras de cada grupo de tratamiento. Las muestras 1 y 2 pertenecen al primer grupo de tratamiento y las muestras 3 y 4 pertenecen al segundo grupo de tratamiento. Los perfiles de expresión de SDHA y CANX se indican en rojo. El perfil de expresión de UBC se indica en amarillo. La tabla enumera los valores Cq medidos en el conjunto de datos.
Debido a la desviación de los perfiles de expresión, es posible que SDHA y CANX estén regulados por las diferentes alternativas de tratamiento y, por lo tanto, no sean adecuados como genes de referencia. Eliminándolos del conjunto de datos y repitiendo el análisis se obtiene un acuerdo entre ambos algoritmos y que la mejor elección de genes de referencia son EIF4A2 y ATP53 (Figura 10.9). En el cálculo de NormFinder de las desviaciones estándar acumuladas, también se aprecia que la adición de más genes de referencia no mejora la estabilidad.
Calculo de las desviaciones estándar acumuladas.
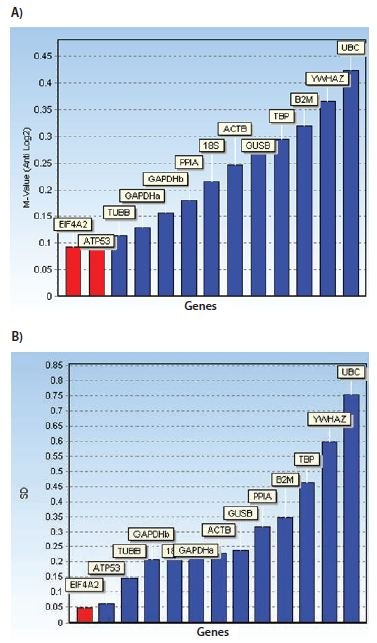
Figura 10.9.La inspección de los perfiles de expresión y de los valores Cq medidos (Figura 10.8) suscitó la preocupación de que SDHA y CANX pudieran estar corregulados en el ensayo aplicado. La corregulación puede alterar los algoritmos de estabilidad del gen de referencia. Diagramas de barras que muestran las medidas de estabilidad: A) valores M para geNorm y B) desviaciones estándar para NormFinder. El conjunto de datos es el mismo que el utilizado en la Figura 10.8, salvo que se han eliminado los datos para SDHA y CANX. Obsérvese que con este conjunto de datos reducido los algoritmos de estabilidad de genes de referencia geNorm y NormFinder coinciden en los mejores genes de referencia.
El análisis de datos de este ejemplo sirve para ilustrar que el uso de geNorm y NormFinder en paralelo permite la identificación de genes de referencia candidatos corregulados y que la eliminación de estos genes de estudios posteriores proporciona una identificación final de genes de referencia que puede adoptarse con más confianza que tras el uso de un único análisis. La identificación y selección de genes de referencia estables conduce a una mayor seguridad del análisis de datos.
Métodos de normalización alternativos
Aunque la normalización a genes de referencia es el método más común para la normalización de ensayos, hay situaciones en las que este enfoque no es adecuado, como cuando se va a comparar un gran número de genes en un grupo heterogéneo de muestras, o cuando se perfilan miRNA. En estos escenarios es necesario adoptar una estrategia alternativa.
Normalización con respecto a la masa tisular o el número de células
La medición del número de células o la masa tisular para utilizarla como factor de normalización no es tan sencilla como puede parecer a primera vista. Los experimentos de cultivo celular son relativamente fáciles de normalizar basándose en el recuento celular. Sin embargo, la adición de un tratamiento puede afectar a la morfología celular, complicando la relación entre el número de células y el ARN/genes totales expresados en comparación con un cultivo de control. El tratamiento experimental puede dar lugar a la producción de matriz extracelular causando diferencias en las eficiencias de extracción de ácidos nucleicos.
Los tejidos biológicos pueden ser muy heterogéneos dentro de los sujetos y entre ellos, siendo más evidente la variación cuando se compara el tejido sano con el tejido enfermo. Incluso los tejidos aparentemente menos complejos, como la sangre, pueden diferir considerablemente en el recuento y la composición celular, de forma que la expresión génica varía considerablemente entre donantes aparentemente sanos18.
Cualquier retraso en los procesos utilizados para purificar el ácido nucleico producirá alteraciones en el ARN medido. Por ejemplo, los retrasos en el procesamiento de las células mononucleares de sangre periférica y en la extracción del ARN de las células producen cambios considerables en la expresión génica19. Los métodos subyacentes a los procedimientos de extracción son también fuentes importantes de variación técnica. Incluso el proceso de aislamiento seleccionado para el muestreo de células derivadas de la sangre y la purificación del ARN dan lugar a diferencias en los perfiles aparentes de expresión génica20. Por lo tanto, la primera consideración de normalización es garantizar que la recogida y el procesamiento sean absolutamente idénticos para todas las muestras. A continuación, es fundamental realizar un control de calidad suficiente para estar seguros de la concentración, integridad y pureza de la muestra (Purificación de muestras y evaluación de la calidad y protocolos asociados en Apéndice A).
Normalización a la concentración de ARN
Como mínimo, una estimación de la concentración de molde (ADN para qPCR o ARN para RT-qPCR) es importante y, como se menciona en&.nbsp;Purificación de muestras y evaluación de la calidad, es fundamental asegurarse de que se utiliza el mismo instrumento para todas las mediciones porque la determinación de la concentración de ácido nucleico también es variable y depende de la técnica.
Cuando se mide la concentración total de ARN, la gran mayoría de la muestra está compuesta por ARNr, y sólo una pequeña fracción está formada por el ARNm de interés cuando se examina la expresión génica, o por el ARNnc cuando se examina la regulación de la expresión génica. Esto significa que si la concentración de ARNr aumenta una pequeña cantidad pero el ARNm permanece constante, la concentración total de ARN aumentará. La concentración de ARNm debe aumentar una cantidad significativa para provocar un aumento aparente de la concentración total de ARN. Por lo tanto, la concentración de ARNr es una medida poco fiable de la concentración de ARNm, pero para muchos protocolos se requiere una concentración igual de ARN para garantizar una transcripción inversa precisa (véase Transcripción inversa).
Normalización a la expresión génica global
Cuando se mide un gran número de dianas, el analista puede estimar la media global de la expresión génica total e identificar las secuencias de ARN reguladas que se desvían de esta media. Este enfoque se utiliza convencionalmente para la normalización de las matrices de expresión génica. Es una alternativa valiosa al uso de genes de referencia y puede ser preferible cuando se miden muchos objetivos.
Otro enfoque explorado recientemente es la medición de elementos repetidos expresados endógenamente (ERE) que están presentes dentro de muchos de los ARNm. Muchas especies contienen estos elementos repetidos (ALU en primates, elementos B en ratones), que pueden proporcionar una estimación de la fracción de ARNm. Se ha demostrado que la medición de estas secuencias diana funciona como los sistemas de normalización convencionales9 (Le Bert, et al., en preparación) y puede ofrecer una solución universal o una alternativa para experimentos complejos en los que no se dispone de combinaciones de genes de referencia estables.
Normalización de datos de miARN
Hasta ahora no se ha informado de un gen de referencia universal de miARN. Por lo tanto, la selección del sistema de normalización sigue siendo más bien empírica. Cuando es posible, se pueden identificar miARNs invariantes estables a partir de enfoques de todo el genoma, es decir, microarrays. También se han utilizado pequeños ARN nucleolares (snoARN) como genes de referencia. La expresión génica global también es un método útil para normalizar la expresión de miARN cuando se desconoce una referencia estable y se han analizado varios cientos de dianas21,22,23. Este método es más apropiado para los que utilizan enfoques que dan lugar a la captura de todos los miARN como ADNc en forma multiplexada, p. ej, sistemas Exiqon y miQPCR (consulte Castoldi et al. en PCR Technologies, Current Innovations24).
Réplicas biológicas y técnicas
El propósito de la normalización es evitar errores sistemáticos y reducir la variabilidad de los datos para el eventual análisis estadístico. Otro aspecto importante de la configuración de los datos para el análisis estadístico es el uso de réplicas de datos.
Las réplicas biológicas son absolutamente necesarias para el análisis estadístico. Los niveles de significación estadística suelen fijarse en un corte de significación del 5%. Para efectos biológicos cercanos a dicho nivel de significación, puede ser necesario tener al menos 20 réplicas biológicas para determinar el nivel de significación de los ensayos (1:20 correspondiente al 5%). De hecho, se ha sugerido que es necesario registrar al menos 50 veces el número de observaciones para una estimación precisa de la significación25, es decir, del orden de mil muestras biológicas. Naturalmente, las limitaciones prácticas rara vez permiten repeticiones biológicas a estos niveles. Además, las estimaciones precisas del número de réplicas biológicas necesarias para alcanzar un determinado nivel de significación también dependen del nivel de variabilidad de los datos. No obstante, es importante tener en cuenta que un error común es subestimar el número necesario de réplicas biológicas para poder llegar a conclusiones fiables. Se recomienda realizar un estudio piloto inicial para evaluar la variabilidad inherente del ensayo y el tamaño potencial del efecto biológico observable con el fin de tener una buena base para estimar el número necesario de réplicas biológicas26.
Las réplicas técnicas no se utilizan directamente para el análisis estadístico. En su lugar, las réplicas técnicas se utilizan para hacer copias de seguridad de las muestras (en caso de que algunas muestras se pierdan en el proceso de manipulación técnica) y para mejorar la evaluación de la precisión de los datos. Las réplicas técnicas pueden mejorar la exactitud de los datos si se cumple el supuesto de que varían estocásticamente en torno a la medición exacta en cada etapa del proceso de manipulación técnica. La media de las réplicas técnicas se aproxima más a la medición exacta. El efecto de promediar las réplicas técnicas puede ilustrarse observando el tamaño del intervalo de confianza en un conjunto de datos simulados con una variabilidad predeterminada, es decir, una desviación estándar fijada en uno. Como se observa en Tabla 10.4, el intervalo de confianza se reduce al aumentar el número de réplicas técnicas (muestras), lo que indica una estimación más precisa de la medición exacta. Además, el estrechamiento del intervalo de confianza es más dramático en el bajo número de réplicas técnicas. Aumentar el número de réplicas de 2-3 disminuye el intervalo de confianza de 8,99-2,48, es decir, una mejora de más de 3 veces de la precisión en la estimación de la medida exacta. Aunque las réplicas adicionales siguen mejorando la estimación de la exactitud de la medición, el efecto es de magnitud decreciente. Por lo tanto, es evidente que en los casos en los que la variabilidad de la manipulación técnica es un problema, puede ser una gran ventaja utilizar triplicados en lugar de duplicados.
Precisión.
Las réplicas técnicas pueden recogerse en varias etapas a lo largo del proceso de manipulación de muestras, incluyendo la extracción de ARN, la transcripción inversa y la detección qPCR. Si se detectan réplicas técnicas en varias etapas, se genera un diseño experimental anidado. Un estudio piloto que aproveche un diseño experimental anidado puede ayudar a identificar las etapas de manipulación de muestras que más contribuyen a los errores técnicos de manipulación y se puede calcular un plan de muestreo óptimo basado en esta información27.
Análisis estadístico y visualización de datos
El análisis científico de datos biológicos se centra en la formulación y comprobación de hipótesis. La formulación de una hipótesis requiere una comprensión detallada de las condiciones y variables del ensayo. La comprobación satisfactoria de una hipótesis implica una ejecución cuidadosa y un diseño experimental adecuado para maximizar la señal observable deseada minimizando al mismo tiempo la variabilidad técnica. En este contexto, es útil distinguir entre estudios exploratorios y confirmatorios (Figura 10.10).
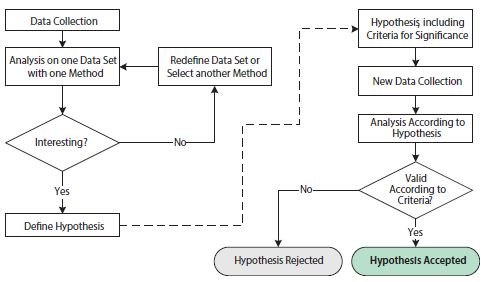
Figura 10.10.Diagrama de flujo que ilustra las operaciones implicadas en los análisis estadísticos exploratorios y confirmatorios. La parte izquierda de la figura, antes de la flecha discontinua, muestra las operaciones de un estudio estadístico exploratorio. La parte derecha de la figura, después de la flecha discontinua, muestra las operaciones de un estudio estadístico confirmatorio.
El propósito del estudio exploratorio es analizar datos con una o varias técnicas diferentes con el fin de corroborar una hipótesis. El conjunto de datos puede redefinirse y/o pueden emplearse repetidamente diferentes técnicas de análisis con el fin de respaldar una o varias hipótesis. El estudio exploratorio es, por tanto, muy flexible a las especificidades de cualquier pregunta científica. Sin embargo, la comprobación repetida de hipótesis sobre un conjunto de datos puede dar lugar a problemas que socaven las conclusiones estadísticas. Esto se debe a las pruebas múltiples, que se refieren al hecho de que una prueba estadística con varias hipótesis independientes tiene más probabilidades de arrojar una significación positiva y que las posibilidades de que esto ocurra aumentan a medida que se prueban hipótesis adicionales, incluso si las distribuciones de probabilidad subyacentes son idénticas. Por ello, para evitar resultados estadísticos engañosos, el estudio exploratorio suele combinarse con un estudio confirmatorio.
Los requisitos de un estudio confirmatorio se basan en criterios estadísticos mucho más estrictos. En primer lugar, la hipótesis de estudio, incluidos los criterios de significación, debe definirse antes de la recogida de datos y antes del análisis. Además, el conjunto de datos para el análisis tiene que haberse recogido exclusivamente para este fin. Es estadísticamente incorrecto reutilizar el conjunto de datos del estudio exploratorio en el estudio confirmatorio, ya que ese conjunto de datos favorecería intrínsecamente la hipótesis propuesta. El resultado final del estudio confirmatorio es una hipótesis rechazada o aceptada según los criterios preestablecidos.
Pruebas estadísticas
Para las pruebas estadísticas, se analiza la probabilidad de que un fenómeno observado haya ocurrido por azar. Esto se denomina hipótesis nula28. Si el fenómeno observado es raro según la hipótesis Nula, la conclusión es que es poco probable que la hipótesis Nula sea válida. Se rechaza la hipótesis Nula y se acepta la probabilidad de que la hipótesis alternativa sea significativa.
La probabilidad estimada de que el fenómeno observado haya ocurrido por azar se denomina valor p. El valor p se mide en un intervalo de 0 a 1, o equivalentemente, en unidades porcentuales. Los criterios estadísticos para un estudio de confirmación incluyen un límite alfa por debajo del cual los valores p calculados indicarían la significación del fenómeno observado. Se suele utilizar un valor de corte alfa del 5%, aunque debe ajustarse para adaptarse a los criterios deseados y necesarios que sean específicos del tema de estudio.
Se han desarrollado muchos algoritmos para calcular los valores p bajo varios supuestos y para diferentes propósitos. Un algoritmo común es la prueba t de Student. La prueba t de Student se utiliza para calcular un valor p basado en la diferencia de los valores medios entre dos grupos de datos. El supuesto principal de la prueba t de Student es que los dos grupos de datos son independientes y se ajustan a distribuciones normales. Una ventaja de la prueba t de Student es que es potente, en comparación con las pruebas estadísticas no paramétricas29. Una prueba no paramétrica equivalente a la prueba t de Student puede ser una de las pruebas estadísticas no paramétricas más conocidas: la prueba de suma de rangos de Wilcoxon (a veces denominada prueba U de Mann-Whitney; no confundir con la prueba de rangos con signo de Wilcoxon, que se utiliza para comparar dos grupos emparejados). Las pruebas estadísticas no paramétricas, como la prueba de suma de rangos de Wilcoxon, tienen la ventaja sobre las pruebas estadísticas paramétricas, como la prueba t de Student, de que no dependen de supuestos previos de las distribuciones del conjunto de datos. Se puede utilizar una prueba de Kolmogorov- Smirnov para la distribución normal para decidir si se aplica la prueba t de Student o una de las pruebas no paramétricas
Además de la elección del algoritmo para&.nbsp;p, los conjuntos de datos que se introducen en el algoritmo de cálculo del valor
pueden manipularse para facilitar la observación de las propiedades deseadas en el conjunto de datos. La combinación de los pasos de manipulación de los datos brutos y la elección del algoritmo de cálculo del valor p forman parte de la construcción de un modelo de hipótesis.
Existe un alto nivel de libertad en la construcción de modelos de hipótesis en la fase exploratoria de un análisis estadístico y esto es una parte importante de la investigación científica. Sin embargo, una hipótesis nunca se demuestra utilizando un enfoque científico y estadístico. Un enfoque científico correcto consiste en formular una hipótesis nula, utilizar un conjunto de datos independientes (preferiblemente recién recogidos) y aceptar o rechazar la hipótesis nula de acuerdo con el diagrama de flujo del estudio confirmatorio (Figura 10.10).
Técnicas de visualización para el análisis univariante
Así como hay muchos métodos de análisis disponibles, también hay muchas técnicas de visualización de datos entre las que elegir. Para el análisis de datos univariantes, un simple diagrama de barras con barras de error asociadas es una técnica de visualización apropiada. Aunque se trata de una técnica de visualización común y sencilla, hay cuestiones que merece la pena destacar. En primer lugar, las barras de error pueden ilustrar diferentes fuentes de variabilidad; la variabilidad inherente de los datos (la desviación estándar, DE) o la precisión con la que se ha determinado el valor medio. En segundo lugar, la precisión con la que se ha determinado el valor medio puede ilustrarse de diferentes formas, pero en última instancia depende de una combinación de la variabilidad inherente de los datos junto con el número de muestras (N) y, en su forma bruta, se denomina error estándar de la media (SEM, Ecuación 1):
Error estándar de la media.
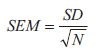
Ecuación 1.SEM
Sin embargo, el SEM no es una medida muy intuitiva y no es sencillo comparar SEMs de diferentes experimentos de forma significativa. Una forma más popular de ilustrar la precisión de la media estimada e indicar la significación estadística de forma gráfica, es el intervalo de confianza (IC, Ecuación 2):
.
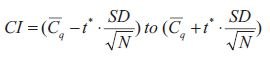
Ecuación 10-2.Cl
La presencia del SEM puede reconocerse en la ecuación del intervalo de confianza como la relación entre la desviación estándar (SD) y la raíz cuadrada del número de muestras (N) y, por tanto, es evidente que el intervalo de confianza se basa en el SEM. El límite inferior del intervalo de confianza se construye restando el SEM multiplicado por un percentil de una distribución t de la media. El límite superior del intervalo de confianza se construye sumando el SEM multiplicado por un percentil de una distribución t a partir de la media. El nivel de confianza del intervalo de confianza se establece mediante el nivel de confianza asociado con el valor crítico t*; típicamente un nivel de confianza del 95%.
Figura 10.11 muestra un gráfico de barras con barras de error que denotan el intervalo de confianza del 95% dentro de cada grupo experimental, destacando la incertidumbre asociada con la estimación media para un ejemplo de expresión génica en muestras de diferentes órganos después del tratamiento con varias dosis de fármacos. Además, se muestran los valores de significación estadística de la prueba t p para la diferencia en la expresión génica entre las muestras de control y cada una de las tres muestras diferentes de diferentes respuestas a dosis de fármacos, indicadas mediante una notación de asterisco. Es habitual que un asterisco corresponda a un pvalor inferior a 0,05, dos asteriscos correspondan a un pvalor inferior a 0,01 y tres asteriscos correspondan a un pvalor inferior a 0,001.
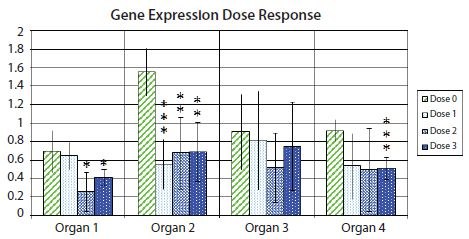
Figura 10.11.Cambio en pliegues (log2) de la expresión de un gen de interés en relación con un par de genes de referencia, en relación con la expresión en la muestra con menor expresión dentro de cada tipo de órgano. Las alturas de las barras indican la expresión media del gen en varias muestras en grupos de muestras no tratadas (Dosis 0) o muestras tratadas con una de las tres dosis diferentes del fármaco (Dosis 1, Dosis 2 y Dosis 3). Las barras de error indican estimaciones del intervalo de confianza del 95% de las expresiones medias. Un asterisco indica una diferencia estadísticamente significativa entre las medias de un conjunto de muestras tratadas en comparación con la media del conjunto de muestras no tratadas al 5%; dos asteriscos indican una diferencia estadísticamente significativa al 1%; tres asteriscos indican una diferencia estadísticamente significativa al 0,1%.
Dado que la notación de asterisco oculta el valor absoluto de p, a menudo se recomienda incluir una tabla con los valores absolutos de p.8125rem;">p, como se muestra en el ejemplo de Tabla 10.5. Uno de los motivos es que un valor p de, por ejemplo, 0,032 es sólo ligeramente más "significativo" que un valor p de 0,055. Casos límite como éste pueden dar lugar a cierta confusión a la hora de decidir con precisión qué punto de corte utilizar para clasificar los datos como significativos. En casos realistas, un valor p de 0,051 podría ser tan significativo como un valor p de 0,049, pero un límite estricto (aunque fundamentalmente arbitrario) de 0,05 clasificaría a uno como significativo y al otro no.
Sin embargo, existe una variante de la visualización del diagrama de barras que aprovecha el intervalo de confianza de la diferencia entre medias para evitar muchas, si no todas, las desventajas de los diagramas de barras tradicionales24. Con el intervalo de confianza de la diferencia entre medias, es posible estimar directamente la significación estadística con barras de error asociadas y, al mismo tiempo, resaltar el tamaño del efecto biológico y la variabilidad de los datos. Figura 10.12 muestra la variante con el intervalo de confianza de la diferencia entre medias de los datos utilizados en Figura 10.11. Observe que los intervalos de confianza que no abarcan la diferencia cero entre medias corresponden a resultados significativos en el nivel de confianza correspondiente al valor de corte (5% en la figura 10.11 y en la tabla 10.5).
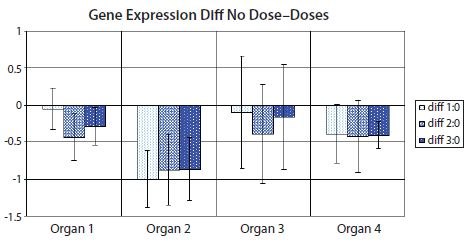
Figura 10.12.Diagrama de barras que muestra la diferencia entre las medias del conjunto de muestras no tratadas (Dosis 0) y uno de los conjuntos de muestras tratadas (Dosis 1, Dosis 2 o Dosis 3) en el conjunto de datos de la Figura 10.11. Las barras de error muestran el intervalo de confianza de la diferencia entre medias. Las barras de error que no cruzan el eje x indican que la comparación de medias correspondiente es estadísticamente significativa al 5% en una prueba t. PCR Technology, Current Innovations-3ª ed. por Taylor and Francis Group LLC Books. Reproducido con permiso de Taylor and Francis Group LLC Books en el formato de reutilización en un libro/libro electrónico a través de Copyright Clearance Center.
Los datos multivariados son datos recogidos sobre varias variables para cada unidad de muestreo. Los datos utilizados en las Figuras 10.11 y;10.12 son multivariantes en el sentido de que dependen de variables como la dosis y el tipo de órgano. Sin embargo, los análisis estadísticos de las figuras 10.11 y 10.12 son univariantes en el sentido de que cada representación (barra) sólo ilustra una variable, la expresión génica, en relación con medidas fijas de las otras variables. Para las técnicas de análisis de datos multivariantes, la agrupación jerárquica y el análisis de componentes principales son buenas opciones para la representación de datos.
Agrupación jerárquica
Uno de los métodos más fáciles y útiles para caracterizar los datos es trazarlos en un diagrama de dispersión (por ejemplo, trazar las medidas de Cq valores de un gen frente a los correspondientes valores Cq de otro gen para un conjunto de muestras biológicas en un gráfico 2D). Los gráficos en una o dos dimensiones son convenientemente visualizados por los ojos humanos. Los gráficos tridimensionales también son posibles con las herramientas adecuadas, pero los gráficos de mayor dimensión son mucho más difíciles de visualizar. Sin embargo, para los estudios exploratorios, el conjunto de datos es intrínsecamente multidimensional y los gráficos de dispersión de conjuntos de datos completos pueden resultar poco prácticos. En un conjunto de datos de qPCR, puede haber, por ejemplo, varios genes y/o varios tipos de muestras biológicas representados.
Una forma popular y alternativa de caracterizar y visualizar datos de estudios exploratorios es analizar medidas de distancias entre puntos de datos en el diagrama de dispersión. Existen diferentes medidas de distancia, incluidas las correlaciones euclidiana, de Manhattan y de Pearson. Con potencia de cálculo, es sencillo calcular distancias, incluso para datos multidimensionales de una dimensionalidad mucho mayor que tres dimensiones. Para la agrupación jerárquica aglomerativa, se realiza el siguiente proceso iterativo: 1) Encontrar los dos objetos más cercanos y fusionarlos en un cluster; 2) Definir el nuevo cluster como un nuevo objeto mediante un método de clustering; 3) Repetir desde 1) hasta que todos los objetos se hayan combinado en clusters30. Entre las alternativas de métodos de agrupación se incluyen el método de Ward, Single linkage y Average linkage31. A menudo se utiliza un dendrograma para visualizar los resultados de la agrupación jerárquica.
La interpretación de los dendrogramas de agrupación jerárquica de los datos de qPCR a menudo da lugar a conclusiones sobre las similitudes de los perfiles de expresión génica. En un estudio exploratorio, estas similitudes pueden utilizarse entonces para formular hipótesis sobre la coregulación de la expresión génica, que pueden aceptarse o rechazarse en estudios confirmatorios posteriores. Las ventajas de los dendrogramas de agrupación jerárquica incluyen la claridad con la que se visualizan las relaciones de similitud. Por otro lado, el fuerte énfasis en las medidas de similitud puede percibirse como limitante con respecto a la formulación de hipótesis, ya que los perfiles de expresión similares pueden ser atributos redundantes en las hipótesis. Puede ser de mayor valor identificar conjuntos de perfiles de expresión que se complementen en una combinación específica, para responder a la hipótesis deseada.
Análisis de Componentes Principales
Otra forma popular y alternativa de caracterizar y visualizar los datos de estudios exploratorios es aprovechar la información contenida en todo el conjunto de datos multidimensionales, seleccionar las propiedades deseadas y proyectarlas a un diagrama de dispersión de menor dimensión, como un gráfico 2D o 3D. Esto puede lograrse mediante el análisis de componentes principales (ACP)32,33,34, 35. Aquí, el sistema de coordenadas original del conjunto de datos (es decir, los perfiles de expresión medidos por qPCR) se transforma en un nuevo espacio multidimensional en el que se construyen nuevas variables (componentes principales: PC o factores). Cada PC es una combinación lineal de los sujetos del conjunto de datos original. Por definición matemática, los PC se extraen en orden sucesivo de importancia. Esto significa que la primera PC explica la mayor parte de la información (varianza) presente en los datos, la segunda menos y así sucesivamente. Por lo tanto, las dos o tres primeras coordenadas de PC (denominadas puntuaciones) pueden utilizarse para obtener una proyección de todo el conjunto de datos en una dimensión convenientemente pequeña, adecuada para su visualización en un gráfico 2D o 3D. Al utilizar las dos o tres primeras PC para la representación, se obtiene la proyección que da cuenta de la mayor variabilidad en el conjunto de datos. Se espera que la varianza de las condiciones de diseño experimental sea sistemática, mientras que se espera que la varianza de confusión sea aleatoria, por lo que esta representación puede ser deseable en condiciones apropiadas.
Como se señaló anteriormente para la agrupación jerárquica, la interpretación del PCA de qPCR a menudo da lugar a conclusiones sobre las similitudes del perfil de expresión génica. Aunque el PCA y la agrupación jerárquica pueden aportar conocimientos complementarios sobre los patrones de corregulación de la expresión génica, ambas técnicas se centran en las similitudes de los perfiles de expresión génica. Esto impone limitaciones a los tipos de hipótesis que pueden hallarse en los estudios exploratorios que utilizan estas técnicas por sí solas. Para ampliar el alcance de las hipótesis generadas en estudios exploratorios, recientemente se propuso un enfoque basado en hipótesis para el análisis multivariante24. Los algoritmos diseñados a medida e impulsados por hipótesis pueden identificar hipótesis biológicamente relevantes que, de otro modo, podrían pasar desapercibidas para las técnicas de análisis multivariante de datos utilizadas habitualmente.
Materiales
Para seguir leyendo, inicie sesión o cree una cuenta.
¿No tiene una cuenta?